Skip to main content

如何给公司估值

· 18 min read

分析公司估值的核心作用​

  • 判断一个相对合理的价格区间。
  • 发现市场中的超跌机会。
  • 稳定盈利的胜负手，是商业模式分析和预测未来趋势。

公司估值的应用场景​

财务类教材，均有介绍公司估值方法​

  • 财务估值是财务管理的核心问题，几乎涉及到每一项财务决策。
  • CPA 的《财务成本管理》，第六章 债券、股票价值评估。

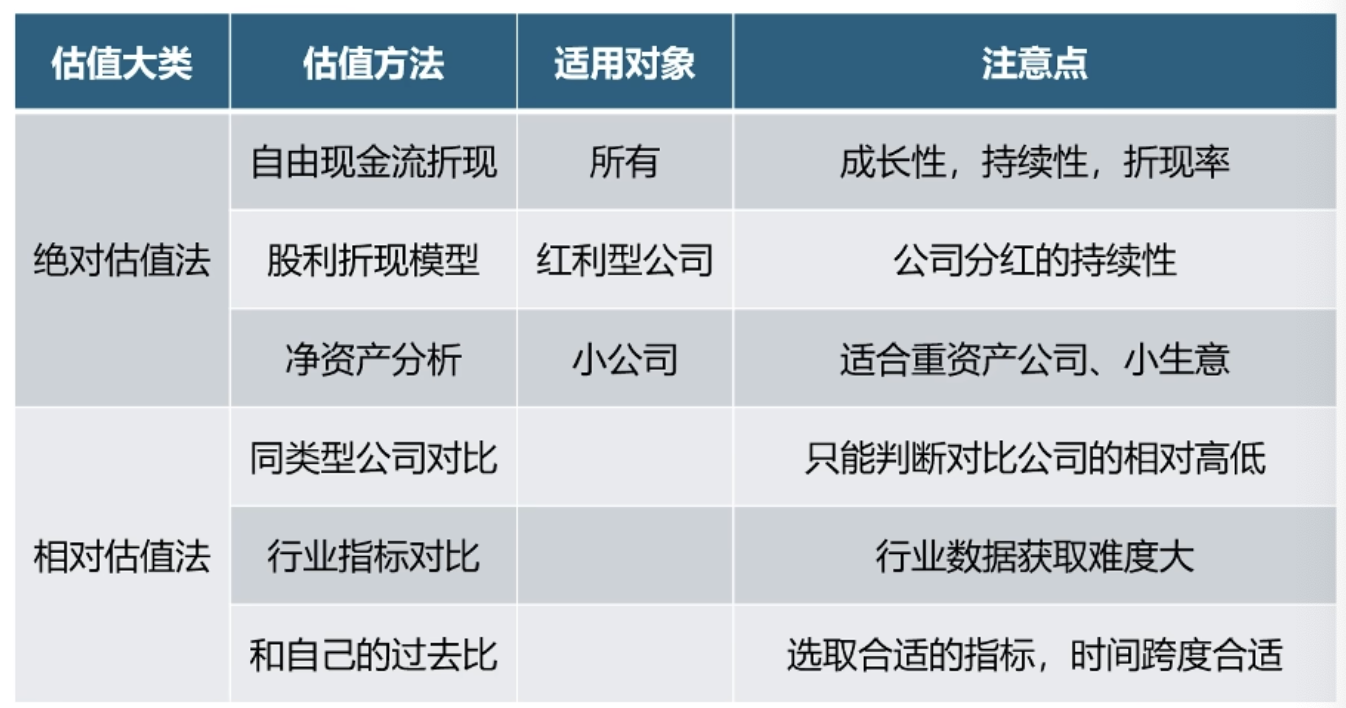
常用的公司估值方法​

  • 绝对估值法
    • 现金流折现法
    • 股利折现模型
    • 净资产分析法
  • 相对估值法
    • 类比估值法 (跟同类公司比)
    • 基于乘数的估值法 (和自己的过去比)

最重要的估值模型，现金流折现法​

  • 现金流折现法
  • 计算未来的钱，放在今天值多少
  • 经典问题，如何给印钞机定价

我们可以把公司的估值问题，简化成一个印钞机估值的问题。除此之外，任何资产都有产生被动现金流的能力，比如说债券，到期可以收取利息，比如说可租赁的房地产，到期可以收取房租。

经典现金流折现问题，如何如何给印钞机定价​

  • 产品名称: 印钞机
  • 产品功能: 每年印钞 10 万元
  • 使用寿命: 10 年

如果是非专业人士，会觉得每年 10 万，10 年就是 100 万。这样的结论忽略了货币的时间价值，在金融上称之为"折现"。

先解释一下什么叫做，现金流折现​

即相同数目的一笔钱，一年后比现在要不值钱。

比如现在的 10 元能买到一杯咖啡，1 年后的 10 元买不到一杯咖啡，所以我应该按照一年后的 10 元的价值给你，如果折现率为 10%的话，通过公式计算10/(1+10%)，我现在应该给你 9.09 左右。

将印钞机未来提供的资金，折现到今天​

折现率 (r): 理论上的合理收益期望，最保守的计算，可以按照无风险利率计算，就是 10 年期国债的收益率。

比如我们给折现率一个 3% 的值。

![[2025-12-13-img-3-how-to-value-a-compnay.png]]

  • 最后我们得到现值: 85.3 万元，所以如果我们要买这台印钞机的话，价格就绝对不能高于 85.3 万。
  • 因为我们现在拿着 85.3 万去买理财，按 3%的利率去算，最后的到的投资结果也是这样的。

所以就没有必要去买这个印钞机，属于是瞎折腾了。如果你没有投资能力，你花 85.3 万买下这个印钞机，基本相当于一个 3%的理财产品。

如果我们的投资能力很强，做别的可以赚更多，那 85.3 万买这个就很不划算了，因为产生了机会成本，所以必须得降价我们才愿意去买。

假设我们的投资收益率达到 8%，那我们的心理预期价格要用 8%的折现率去计算，算下来的结果大约是 67.1 万元。

现金流折现法，是给资产估值的通用方法​

  • 债券
    • 利息是债券提供的现金流
  • 固定资产
    • 租金是固定资产的现金流
  • 公司
    • 利润是公司赚到的现金流

比如债券，如果初始价格是 200 万，每天产生 10 万现金流，10 年后退回 200 万，就相当于一个年化 5%的债券。

如果中间我们不想再持有债券了，就相当于要卖掉手里的印钞机，那这个二手印钞机的定价问题，就是现在债券市场的定价。

对于固定资产和公司都是一样的，公司是一个具有成长性的印钞机 (公司的利润可以每年增加，也可以是每年降低)。

影响资产估值的三个变量​

![[2025-12-13-img-4-how-to-value-a-compnay.png]]

折现率的选择，无风险利率 + 风险溢价​

![[2025-12-13-img-5-how-to-value-a-compnay.png]]

  • 折现率可以理解为，投资者要求的必要回报率。

长江电力估值分析案例，持续性对估值的影响​

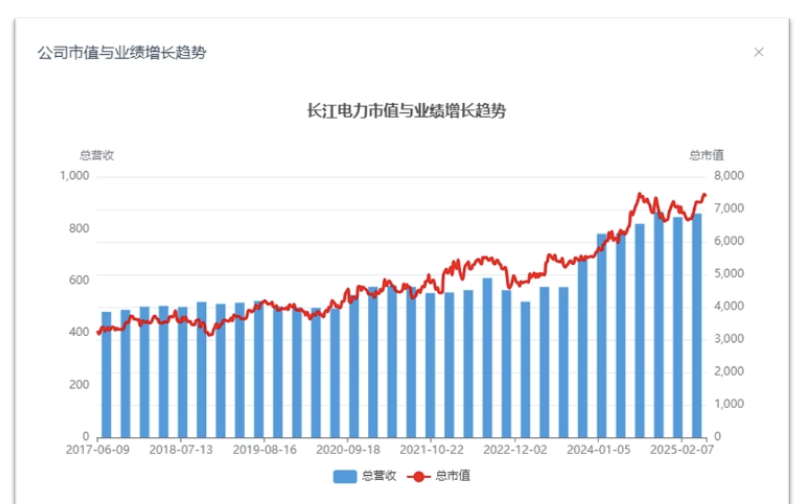
![[2025-12-13-img-6-how-to-value-a-compnay.png]]

@TODO

贵州茅台估值分析案例，成长性对估值的影响​

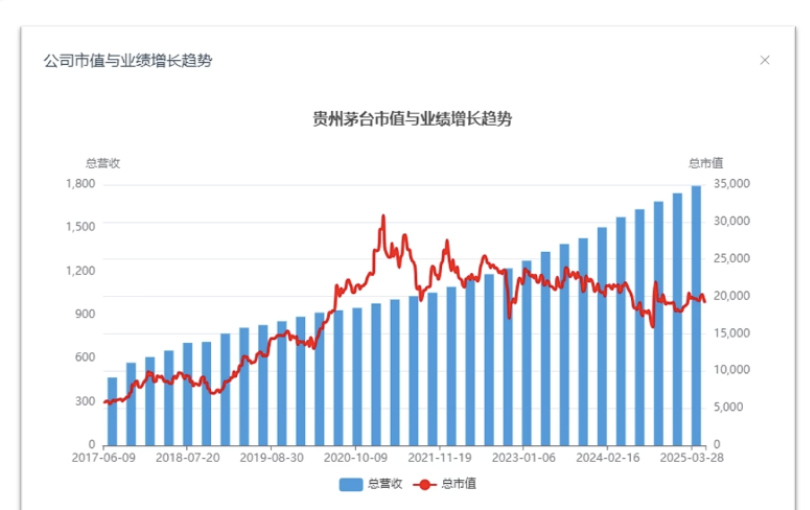
![[2025-12-13-img-7-how-to-value-a-compnay.png]]

@TODO

现金流折现需要预设未来，本身就存在不确定性​

  • 成长性和持续性，属于对未来预测
  • 对未来的预测，直接影响现在的估值
  • 悲观和乐观的预测，都是合理范围

@TODO

未来能赚多少，不能看净利润，看自由现金流​

![[2025-12-13-img-8-how-to-value-a-compnay.png]]

  • 自由现金流: 企业实际可以自由支配的资金。
  • 经营现金流净额是现金流量表中一个比较重要的项目。
  • 资本支出: 公司购置或升级长期资产的现金支出，在现金流量表的投资活动中体现。

关于企业自由现金流的两个案例​

  • 安琪酵母
    • 赚的钱都拿去建工厂了
    • 没有自由现金流
  • 长江电力
    • 成本大头是固定资产折旧
    • 自由现金流非常高

列举计算模型清单​

戈登增长模型 (永续经营)​

戈登增长模型 (此模型将默认为永续经营，所以没有代入 n)

[P0=D0×(1+g)r−g][ P_0 = \frac{D_0 \times (1+g)}{r - g} ] [永续价值 (TV)=FCF0×(1+g)r−g][ \text{永续价值 (TV)} = \frac{FCF_0 \times (1+g)}{r - g} ]

(有限期)增长年金公式​

标准公式​

用于计算一系列按固定增长率增长、持续有限期的现金流现值。

公式 1（现金流从第 1 期期末开始，持续 n 期）：[PV=C1×1−(1+g1+r)nr−g,r≠g][ PV = C_1 \times \frac{1 - \left( \frac{1+g}{1+r} \right)^n}{r - g}, \quad r \neq g ] 其中：

  • ( C_1 ) = 第 1 期末的现金流
  • ( g ) = 每期增长率
  • ( r ) = 每期折现率
  • ( n ) = 现金流期数

公式 2（现金流从第 0 期开始，即立即开始，持续 n 期）： [PV=C0×(1+g)×1−(1+g1+r)nr−g,r≠g][ PV = C_0 \times (1+g) \times \frac{1 - \left( \frac{1+g}{1+r} \right)^n}{r - g}, \quad r \neq g ] 其中 ( C_0 ) = 第 0 期（当前）现金流。

特殊情况（当 ( r = g ) 时）： [PV=n×C11+r或PV=n×C0][ PV = \frac{n \times C_1}{1+r} \quad \text{或} \quad PV = n \times C_0 ] （取决于现金流起始时间）

公式推导​

假设现金流从第 1 年末开始，每年增长 g，持续 n 年：

[PV=C11+r+C1(1+g)(1+r)2+⋯+C1(1+g)n−1(1+r)n][ PV = \frac{C_1}{1+r} + \frac{C_1(1+g)}{(1+r)^2} + \cdots + \frac{C_1(1+g)^{n-1}}{(1+r)^n} ] 提取公因子 (C11+r)( \frac{C_1}{1+r} )，括号内为等比数列，公比 (q=1+g1+r)( q = \frac{1+g}{1+r} )： [PV=C11+r×1−qn1−q=C1×1−(1+g1+r)nr−g][ PV = \frac{C_1}{1+r} \times \frac{1 - q^n}{1 - q} = C_1 \times \frac{1 - \left( \frac{1+g}{1+r} \right)^n}{r - g} ]

逐年折现剩余年限的现金流方法​

标准公式​

当现金流增长率不恒定或需要精确计算时，采用逐年折现。

基本折现公式： [PV=∑t=1nCFt(1+r)t][ PV = \sum_{t=1}^{n} \frac{CF_t}{(1+r)^t} ] 其中：

  • ( CF_t ) = 第 t 期的现金流
  • ( r ) = 折现率
  • ( n ) = 总期数

通过自由现金流，来计算茅台的估值​

{预期说明}

用自由现金流折现法计算一下公司当前的合理估值是多少？

普通预期 (五年 10%)​

  • 茅台公司
  • 自由现金流: 836 亿
  • 折现率: 8%
  • 成长性
    • 五年内 10%
    • 永续经营 3%
  • 持续时间
    • 永续经营 50 年

根据两阶段自由现金流折现模型，假设前 5 年自由现金流按 10%增长，之后按 3%永续增长，折现率为 8%，当前自由现金流为 836 亿元，计算过程如下：

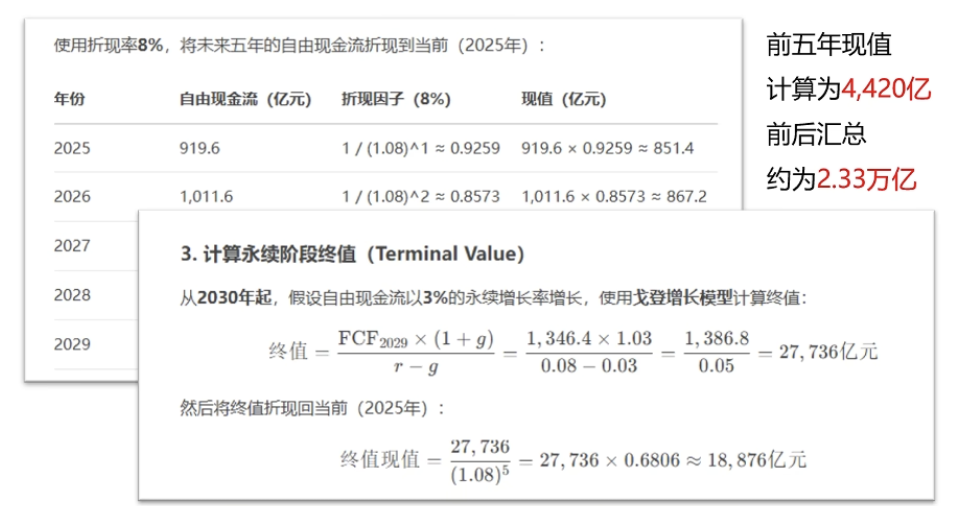
![[2025-12-13-img-9-how-to-value-a-compnay.png]]

1. 预测前 5 年自由现金流（单位：亿元）​

  • 第 1 年：836 × 1.10 = 919.60
  • 第 2 年：836 × 1.10² = 1011.56
  • 第 3 年：836 × 1.10³ = 1112.72
  • 第 4 年：836 × 1.10⁴ = 1223.99
  • 第 5 年：836 × 1.10⁵ = 1346.19

2. 计算前 5 年现金流现值（折现率 8%）​

  • 第 1 年现值：919.60 ÷ 1.08 = 851.48
  • 第 2 年现值：1011.56 ÷ 1.08² = 867.19
  • 第 3 年现值：1112.72 ÷ 1.08³ = 883.18
  • 第 4 年现值：1223.99 ÷ 1.08⁴ = 899.42
  • 第 5 年现值：1346.19 ÷ 1.08⁵ = 916.12

前 5 年现值合计：851.48 + 867.19 + 883.18 + 899.42 + 916.12 = 4417.39

3. 计算永续价值（终值）及现值​

  • 第 5 年末终值（戈登增长模型）：$$ ( TV = 1346.19 \times \frac1.030.05 = 1346.19 \times 20.6 = 27731.43 )
  • 终值现值：27731.43 ÷ 1.08⁵ = 27731.43 ÷ 1.46933 = 18873.50

4. 公司合理估值​

[总现值=4417.39+18873.50=23290.89≈23291亿元][ 总现值 = 4417.39 + 18873.50 = 23290.89 \approx 23291 亿元 ]

茅台公司当前的合理估值约为  23291 亿元。

5. 计算公司合理股价​

茅台的当前总股本是 12.52 亿，那计算出来的合理股价就是 1860 元每股。

乐观预期 (五年 15%)​

  • 茅台公司
  • 自由现金流: 836 亿
  • 折现率: 8%
  • 成长性
    • 五年内 15%
    • 永续经营 3%
  • 持续时间
    • 永续经营 50 年

根据两阶段自由现金流折现模型，假设前 5 年自由现金流按 15%增长，之后按 3%永续增长，折现率为 8%，当前自由现金流为 836 亿元，计算过程如下：

1. 预测前 5 年自由现金流（单位：亿元）​

  • 第 1 年：836 × 1.15 = 961.40
  • 第 2 年：836 × 1.15² = 1105.61
  • 第 3 年：836 × 1.15³ = 1271.45
  • 第 4 年：836 × 1.15⁴ = 1462.17
  • 第 5 年：836 × 1.15⁵ = 1681.49

2. 计算前 5 年现金流现值（折现率 8%）​

  • 第 1 年现值：961.40 ÷ 1.08 = 890.19
  • 第 2 年现值：1105.61 ÷ 1.08² = 947.84
  • 第 3 年现值：1271.45 ÷ 1.08³ = 1009.30
  • 第 4 年现值：1462.17 ÷ 1.08⁴ = 1074.80
  • 第 5 年现值：1681.49 ÷ 1.08⁵ = 1144.38

前 5 年现值合计：890.19 + 947.84 + 1009.30 + 1074.80 + 1144.38 = 5066.51

3. 计算永续价值（终值）及现值​

  • 第 6 年自由现金流：1681.49 × 1.03 = 1731.94
  • 第 5 年末终值（戈登增长模型）：$$ ( TV_5 = \frac1731.940.05 = \frac1731.940.05 = 34638.80 )
  • 终值现值：34638.80 ÷ 1.08⁵ = 34638.80 ÷ 1.46933 = 23574.85

4. 公司合理估值​

[总现值=5066.51+23574.85=28641.36≈28641亿元][ 总现值 = 5066.51 + 23574.85 = 28641.36 \approx 28641 亿元 ]

因此，茅台公司当前的合理估值约为  28641 亿元。

5. 计算公司合理股价​

茅台的当前总股本是 12.52 亿，那计算出来的合理股价就是 2288 元每股。

悲观预期 (五年 8%)​

  • 茅台公司
  • 自由现金流: 836 亿
  • 折现率: 8%
  • 成长性
    • 五年内 8%
    • 永续经营 3%
  • 持续时间
    • 永续经营 50 年

根据两阶段自由现金流折现模型，假设前 5 年自由现金流按 8%增长，之后按 3%永续增长，折现率为 8%，当前自由现金流为 836 亿元。计算过程如下：

1. 预测前 5 年自由现金流（单位：亿元）​

  • 第 1 年：836 × 1.08 = 902.88
  • 第 2 年：836 × 1.08² = 975.11
  • 第 3 年：836 × 1.08³ = 1053.12
  • 第 4 年：836 × 1.08⁴ = 1137.37
  • 第 5 年：836 × 1.08⁵ = 1228.36

2. 计算前 5 年现金流现值（折现率 8%）​

  • 第 1 年现值：902.88 ÷ 1.08 = 836.00
  • 第 2 年现值：975.11 ÷ 1.08² = 836.00
  • 第 3 年现值：1053.12 ÷ 1.08³ = 836.00
  • 第 4 年现值：1137.37 ÷ 1.08⁴ = 836.00
  • 第 5 年现值：1228.36 ÷ 1.08⁵ = 836.00

前 5 年现值合计：836 × 5 = 4180.00

3. 计算永续价值（终值）及现值​

  • 第 6 年自由现金流：1228.36 × 1.03 = 1265.21
  • 第 5 年末终值（戈登增长模型）： [TV5=1265.210.08−0.03=1265.210.05=25304.20][ TV_5 = \frac{1265.21}{0.08 - 0.03} = \frac{1265.21}{0.05} = 25304.20 ]
  • 终值现值：25304.20 ÷ 1.08⁵ = 25304.20 ÷ 1.46933 ≈ 17221.27

4. 公司合理估值​

[总现值=4180.00+17221.27=21401.27≈21401亿元][总现值 = 4180.00 + 17221.27 = 21401.27 \approx 21401 亿元]

因此，茅台公司当前的合理估值约为 21401 亿元。

5. 计算公司合理股价​

茅台的当前总股本是 12.52 亿，那计算出来的合理股价就是 1709 元每股。

综合判断​

大家可以根据自己的商业判断，去调整参数，再结合其他集中估值方式。

最终评估给它的合理区间是 1500-2000 元之间。

除了现金流折现法，还需要了解几个估值方法​

常用的公司估值方法

在实际操作中，我们一般是所有方法都尽量求测算一下，然后综合考虑，交叉验证，得到一个相对合理的估值区间，还有集中比较常见的估值方法，分别是:

  • 股利折现模型
  • 净资产分析法
  • 类比估算法

股利折现模式，适用于红利类公司​

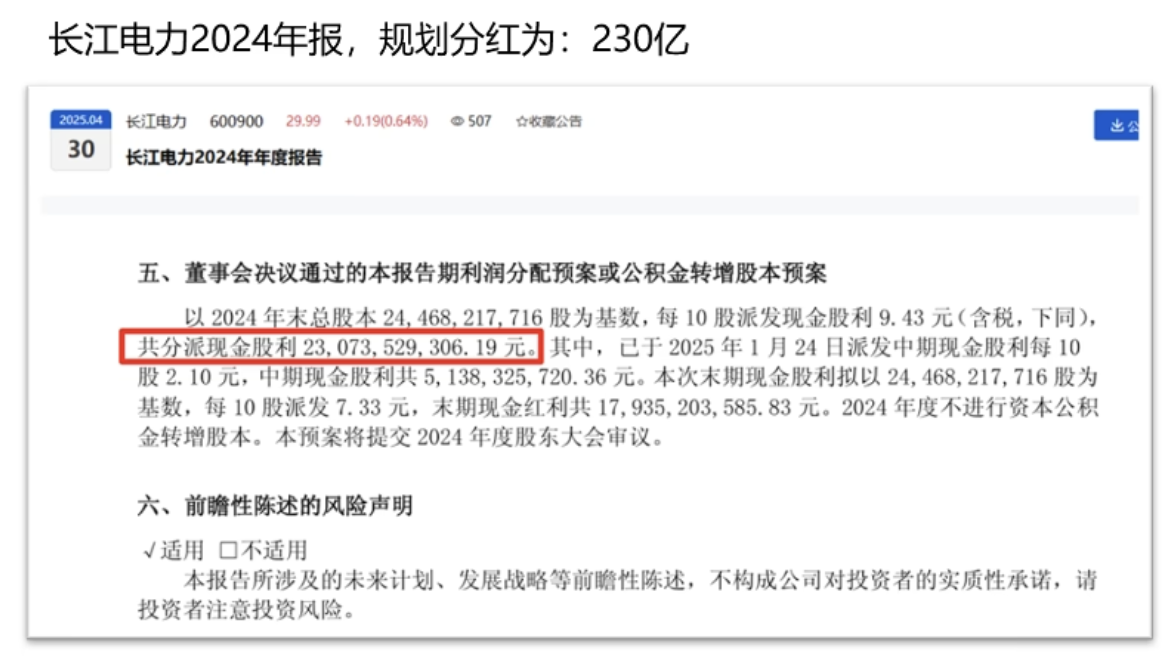
![[2025-12-13-img-10-how-to-value-a-compnay.png]]

增长年金公式计算​

  • 长江电力
  • 自由现金流: 230 亿
  • 折现率: 5.5%
  • 成长性
    • 五年内 2%
    • 永续经营 2%
  • 持续时间
    • 永续经营 100 年

根据两阶段自由现金流折现模型，假设第一阶段为 5 年，自由现金流按 2%增长；第二阶段为 100 年（第 6 年至第 105 年），自由现金流按 2%增长；折现率为 5.5%，当前自由现金流为 230 亿元。计算公司合理估值如下：

1. 第一阶段（第 1-5 年）现金流现值​

  • 预测现金流（亿元）并折现：
    • 第 1 年：230 × 1.02 = 234.60，现值：234.60 / 1.055 ≈ 222.37
    • 第 2 年：230 × 1.02² = 239.29，现值：239.29 / 1.055² ≈ 215.00
    • 第 3 年：230 × 1.02³ = 244.08，现值：244.08 / 1.055³ ≈ 207.86
    • 第 4 年：230 × 1.02⁴ = 248.96，现值：248.96 / 1.055⁴ ≈ 201.02
    • 第 5 年：230 × 1.02⁵ = 253.94，现值：253.94 / 1.055⁵ ≈ 194.37
  • 第一阶段现值合计：222.37 + 215.00 + 207.86 + 201.02 + 194.37 = 1040.62

2. 第二阶段（第 6-105 年）现金流现值​

  • 第 6 年现金流：253.94 × 1.02 = 259.02
  • 第 5 年末现值（增长年金公式）： [PV5=259.02×1−(1.021.055)1000.055−0.02≈259.02×1−0.034170.035≈259.02×27.595≈7147.6][ PV_5 = 259.02 \times \frac{1 - \left( \frac{1.02}{1.055} \right)^{100}}{0.055 - 0.02} \approx 259.02 \times \frac{1 - 0.03417}{0.035} \approx 259.02 \times 27.595 \approx 7147.6 ]
  • 折现至当前：7147.6 / 1.055⁵ ≈ 7147.6 / 1.30643 ≈ 5470.8

3. 公司合理估值​

[总现值=1040.62+5470.8=6511.42≈6511亿元][ 总现值 = 1040.62 + 5470.8 = 6511.42 \approx 6511 亿元 ]

因此，长江电力当前的合理估值约为  6511 亿元。
（注：假设第二阶段持续 100 年；若为无限期永续增长，估值约为 6703 亿元。）

4. 计算公司合理股价​

长江电力的当前总股本是 244.68 亿，那计算出来的合理股价就是 26.61 元每股。

(永续经营)戈登增长模型​

  • 长江电力
  • 自由现金流: 230 亿
  • 折现率: 5.5%
  • 成长性
    • 五年内 2%
    • 永续经营 2%
  • 持续时间
    • 永续经营 (永久)

若第二阶段为无限期永续增长，则使用戈登增长模型计算永续价值。具体计算调整如下：

1. 第一阶段（前 5 年）现金流现值​

  • 预测现金流（亿元）并折现（增长率 2%，折现率 5.5%）：
    • 第 1 年：230 × 1.02 = 234.60，现值：234.60 / 1.055 ≈ 222.37
    • 第 2 年：230 × 1.02² = 239.29，现值：239.29 / 1.055² ≈ 215.00
    • 第 3 年：230 × 1.02³ = 244.08，现值：244.08 / 1.055³ ≈ 207.86
    • 第 4 年：230 × 1.02⁴ = 248.96，现值：248.96 / 1.055⁴ ≈ 201.02
    • 第 5 年：230 × 1.02⁵ = 253.94，现值：253.94 / 1.055⁵ ≈ 194.37
  • 第一阶段现值合计：222.37 + 215.00 + 207.86 + 201.02 + 194.37 = 1040.62 亿元

2. 第二阶段（永续增长）终值及现值​

  • 第 6 年现金流：253.94 × 1.02 ≈ 259.02 亿元
  • 第 5 年末终值（戈登增长模型）： [TV5=C6r−g=259.020.055−0.02=259.020.035≈7400.57亿元][ TV_5 = \frac{C_6}{r - g} = \frac{259.02}{0.055 - 0.02} = \frac{259.02}{0.035} \approx 7400.57 亿元 ]
  • 终值折现至当前： [PVterminal=7400.57(1.055)5≈7400.571.30643≈5664.6亿元][ PV_{\text{terminal}} = \frac{7400.57}{(1.055)^5} \approx \frac{7400.57}{1.30643} \approx 5664.6 亿元 ]

3. 公司合理估值​

[总现值=1040.62+5664.6=6705.22≈6705亿元][ 总现值 = 1040.62 + 5664.6 = 6705.22 \approx 6705 亿元 ]

因此，在无限期永续增长假设下，长江电力的合理估值约为  6705 亿元。

4. 计算公司合理股价​

长江电力的当前总股本是 244.68 亿，那计算出来的合理股价就是 27.4 元每股。

对比说明两种计算模型​

  • 100 年有限期：估值约 6511 亿元，当前合理股价 26.61 每股（因 100 年后现金流被截断，忽略部分现值）。
  • 无限期永续：估值约 6705 亿元，当前合理股价 27.4 每股（包含所有未来现金流现值）。

两者差异约 194 亿元，主要来自 100 年后的现金流现值。当永续增长率（g）低于折现率（r）时，无限期模型收敛为有限值，且后续年份现值随年限增加迅速减小（因折现效应）。

净资产估值法，适用于小生意​

  • 对于上市公司，净资产不能完全反映企业价值
  • 适用于小型生意
  • 适用于中资产公司

@TODO

案例分析，茅台的市净率趋势图​

![[2025-12-13-img-11-how-to-value-a-compnay.png]]

  • 平均值
  • 标准差

相对估值法，类比估算，适用于初步快速评估​

  • 茅台 vs 五粮液

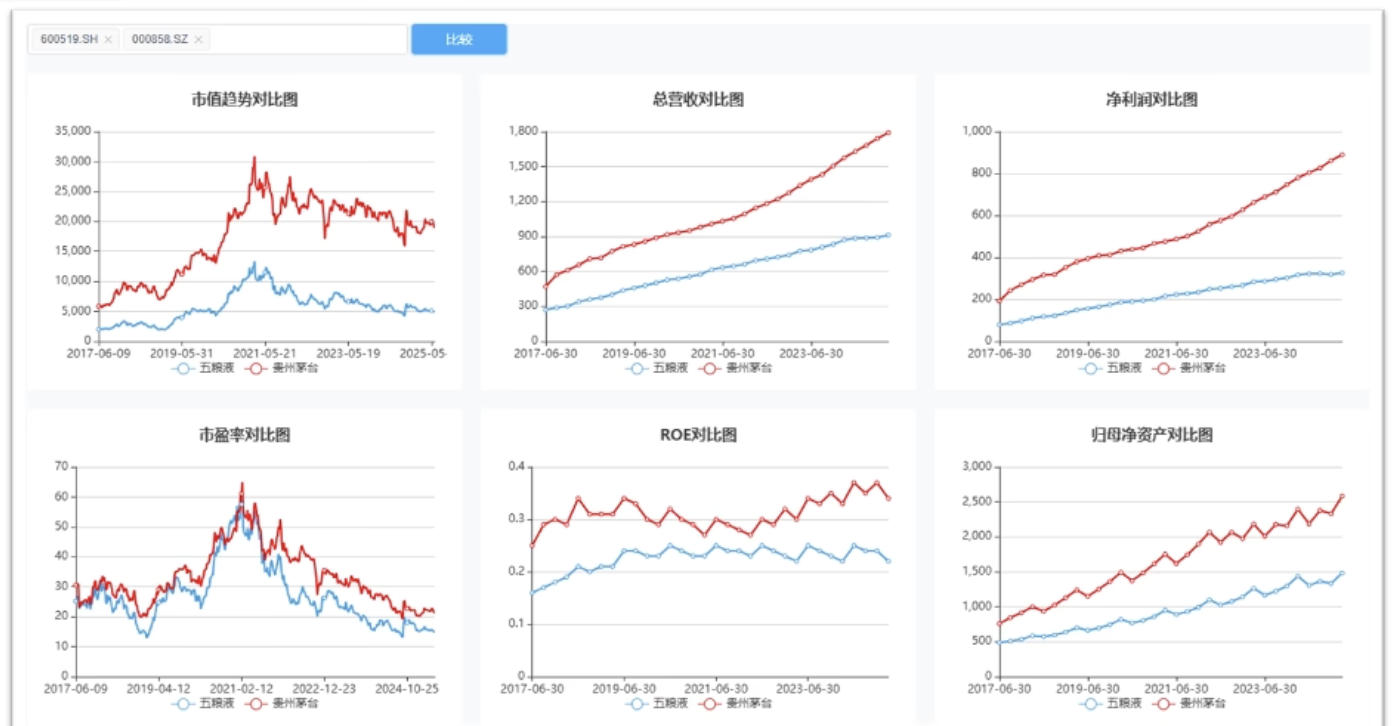
![[2025-12-13-img-12-how-to-value-a-compnay.png]]

类比估算法的局限性

  • 同类型的公司对比，我们只能判断这两个公司的估值相对高低
  • 但如果这个行业本身就估值偏高或这两个对比的公司的估值都偏低了呢？

所以我们必须保证参考目标的估值是合理的，否则得到的结论意义就不是很大，这种估值方法适用于快速评估。

比如在上面的例子中，茅台作为白酒行业最好的公司，当前市盈率是 22，同类型公司 PE 只要超过茅台，基本就不用考虑了。

和同类型公司对比，也可以和行业进行对比​

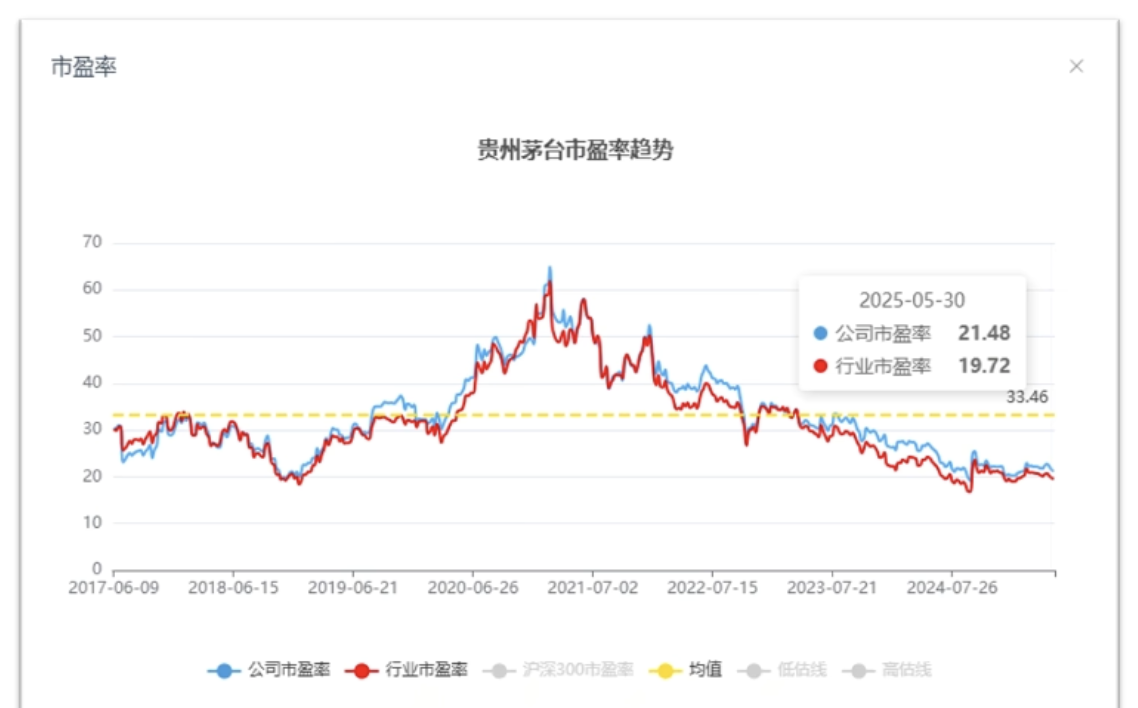
![[2025-12-13-img-13-how-to-value-a-compnay.png]]

  • 茅台市盈率 21.48，行业市盈率 19.72。
  • 通过这个指标解读，考虑到茅台的行业地位，茅台的估值和行业的估值相比，茅台的估值偏低了。
  • 其他的数据也可以这样对比，比如市净率，市销率。

和同类型公司对比，也可以和自己的过去对比​

茅台过去 8️⃣ 年的市盈率走势图

  • 计算平均值
  • 计算标准差
  • 花一个标准差作为高估和低估的参考线

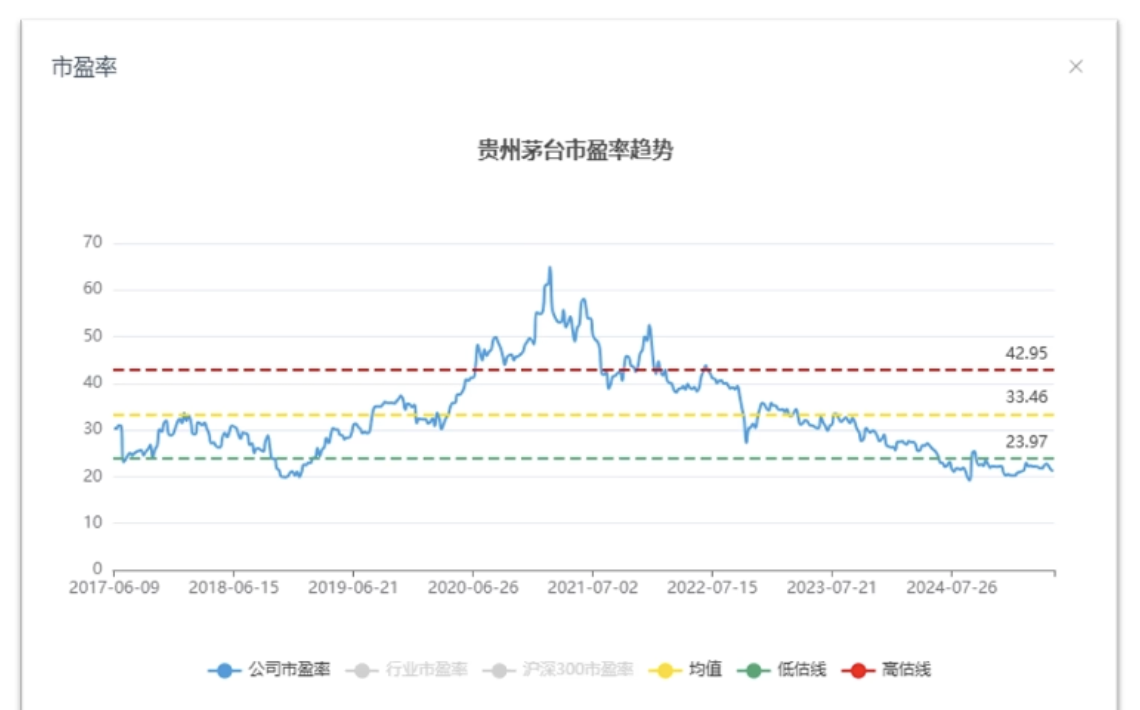
![[2025-12-13-img-14-how-to-value-a-compnay.png]]

  • 这里我们使用市盈率作为对比指标，但市盈率只适合业绩和利润相对稳定的大型公司。
  • 中小型公司的战略，不一定以利润指标为主，他们可能为了成长性的战略目标适当的降低公司对利润的追求，所以利润不稳定的中小型公司和成长型公司，市盈率就不太适用。
  • 我们可以改为市净率和市销率作为估值的对比分析。

重点都是观察公司的市值是否合适，利润稳定的大型公司适合用市盈率，中资产公司适合用市净率，告诉成长型公司用市销率会更好一点。

市场乐观的时候，指标偏高，市场悲观的时候，指标偏低，但我们拉长时间看，指标一定会在一个相对合理的区间内来回波动。

考虑到公司的成长性，时间区间的选取差不多 8️⃣ 年就可以了。

公司估值总结​

![[2025-12-13-img-15-how-to-value-a-compnay.png]]