类神经网络训练不起来怎么办？

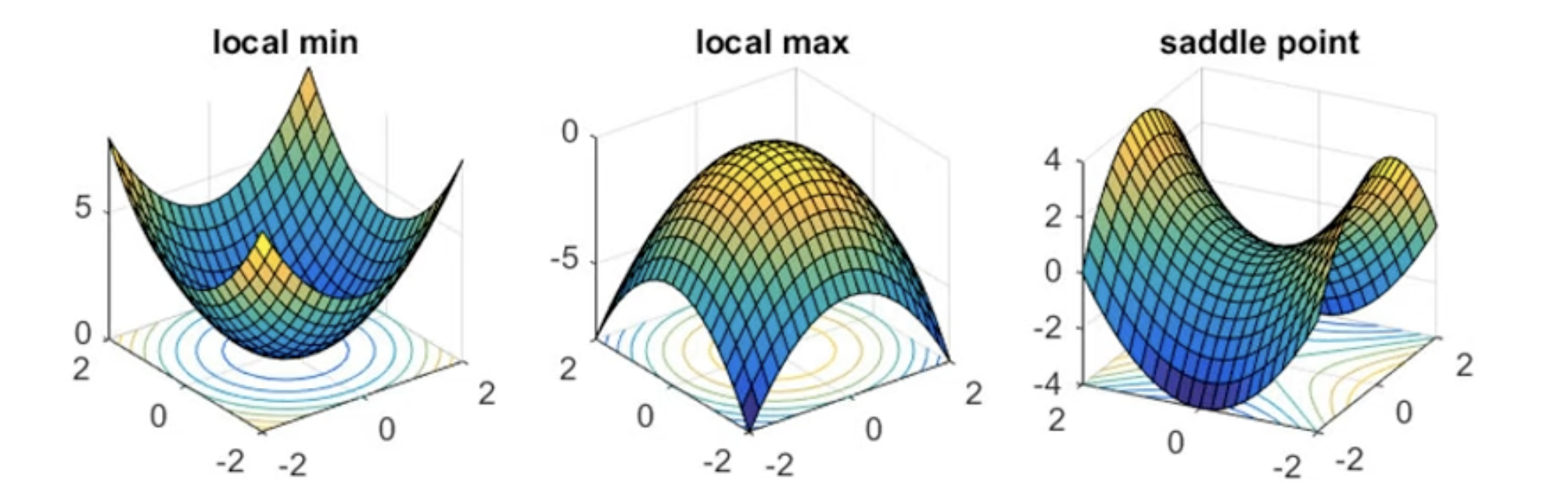
Critical Points

• Local minima
• Local maxima
• Saddle point (马鞍)

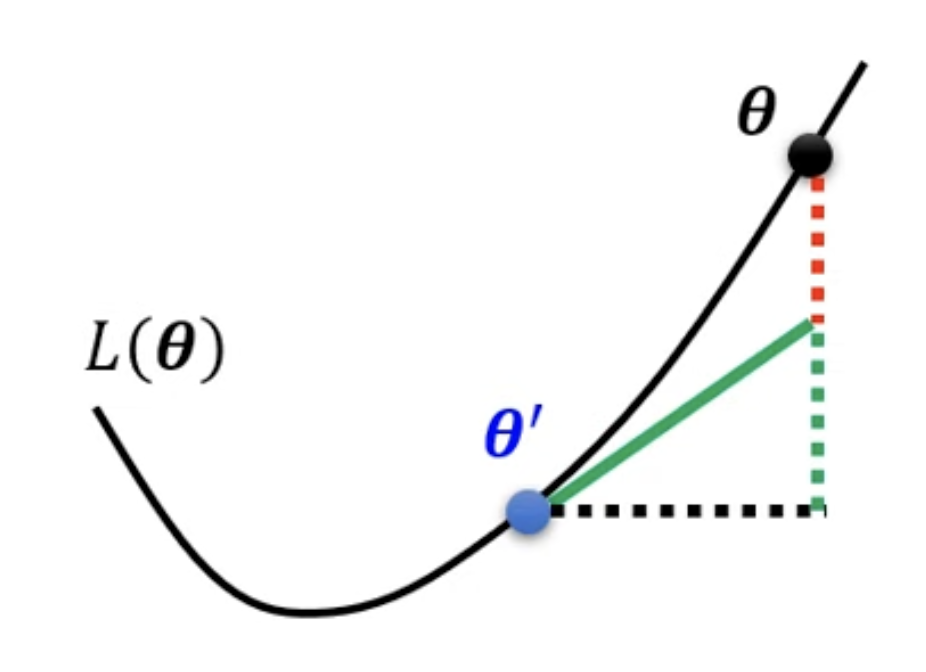
Tayler Series Approximation

The loss function $( L(\theta) )$ around $( \theta = \theta' )$ can be approximated as:

$$[ L(\theta) \approx L(\theta') + (\theta - \theta')^T g + \frac{1}{2} (\theta - \theta')^T H(\theta - \theta') ]$$

Gradient ( g ) is a vector:

$$[ g = \nabla L(\theta') \quad \text{where} \quad g_i = \frac{\partial L(\theta')}{\partial \theta_i} ]$$

Hessian ( H ) is a matrix:

$$[ H\_{ij} = \frac{\partial^2}{\partial \theta_i \partial \theta_j} L(\theta') ]$$

No local minima

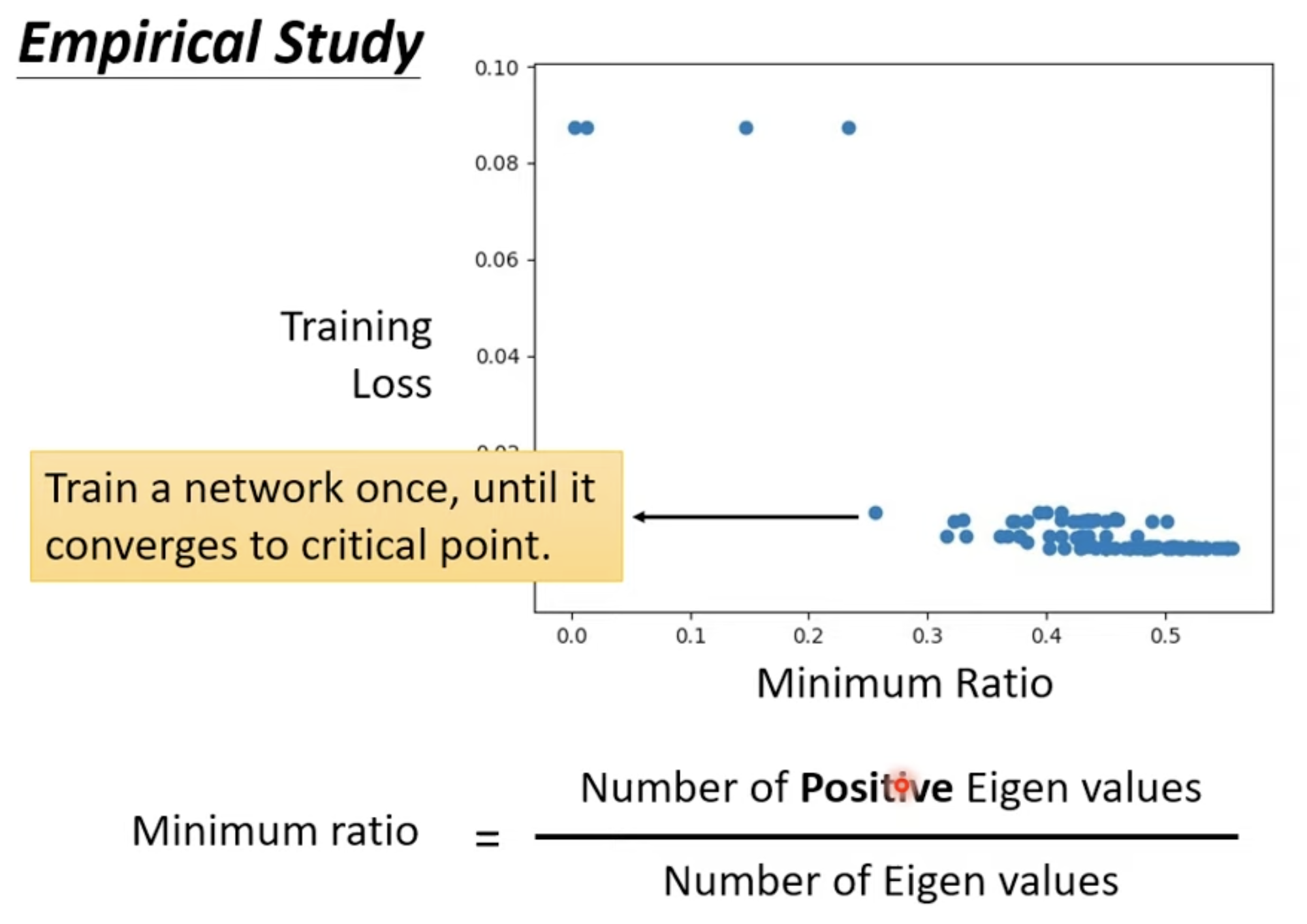
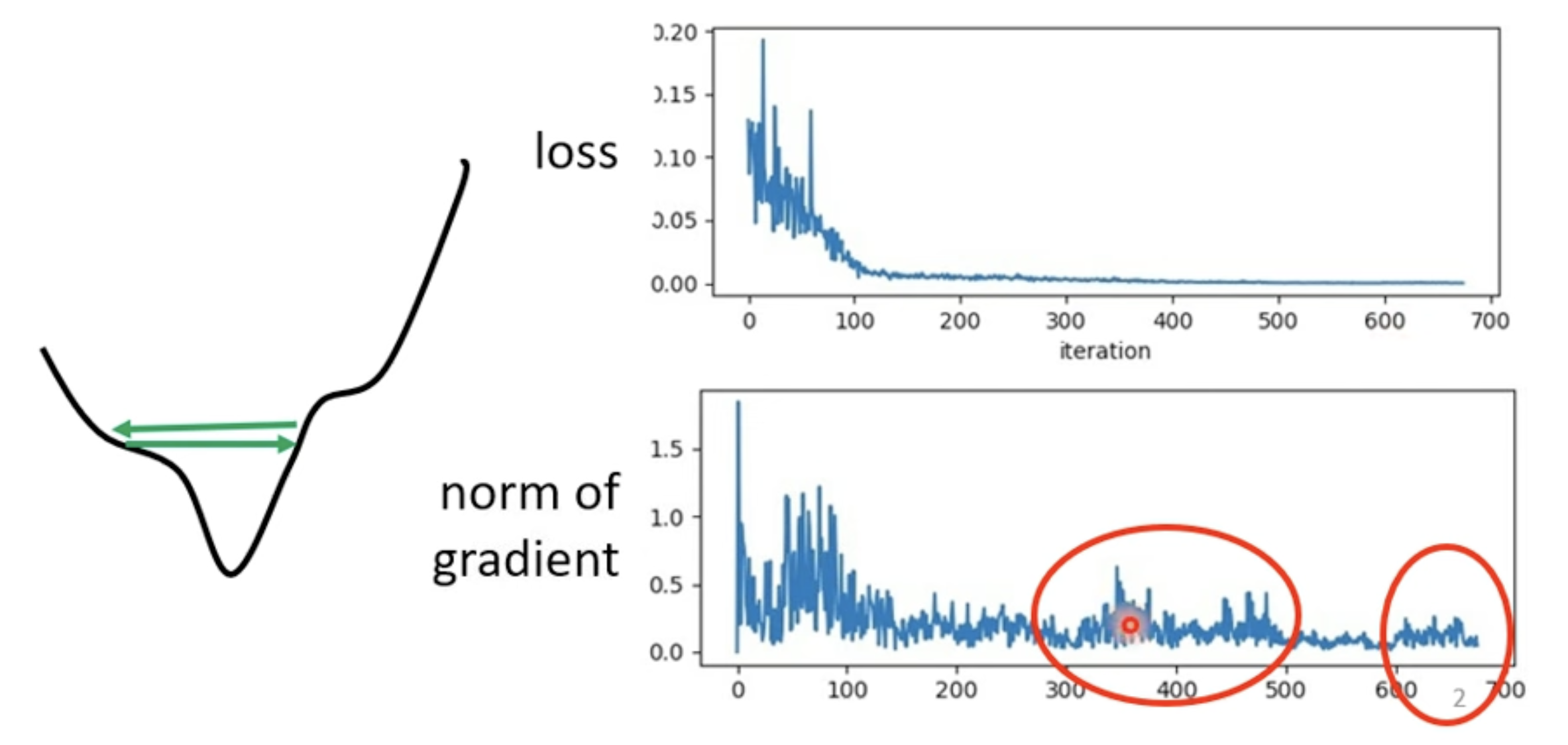
根据研究，我们其实很难找到 local minima, 因为 minimum ration 和图上的研究，我们获得最好的 Loss 的时候， Minimum Ration 大概就在 0.6 左右，这意味着我们其实还可以继续往 loss 更低的方向继续走；但是为什么训练可以停下来了呢，一个是成本问题，继续往下训练带来的成本增加和获得效果不成正比，二是你可能卡在了一个 saddle point.

Training stuck != Small Gradient

• [[blog/2025-06-30-blog-082-machine-learning-training-guide/index#训练技术#Adaptive Learning Rate 技术]]

With Root Mean Square

Optimizers

Adam: RMSProp + Momentum

• [[blog/2025-06-30-blog-082-machine-learning-training-guide/index#训练技术#Adaptive Learning Rate 技术#RMSProp]]
• [[blog/2025-06-30-blog-082-machine-learning-training-guide/index#训练技术#Momentum 技术]]

Summary of optimization

• 算不同的 momentum
• 算不同的 $\sigma$
• 算不通的 $\eta$

训练技术

Batch 技术: Small Batch vs. Large Batch

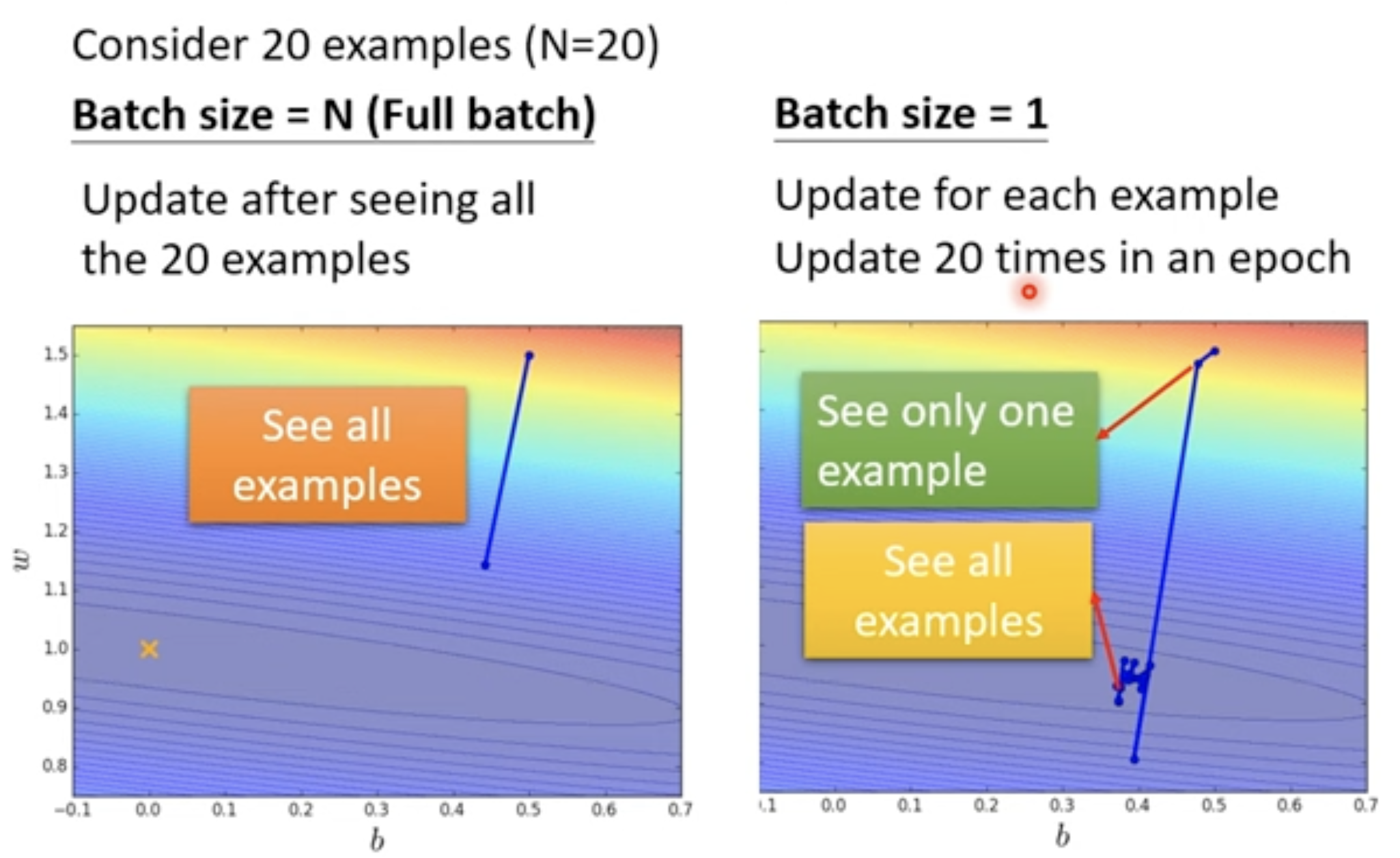
Metric	Small Batch	Large Batch
Speed for one update (no parallel)	Faster	Slower
Speed for one update (with parallel)	Same	Same (not too large)
Time for one epoch	Slower	Faster ✅
Gradient	Noisy	Stable
Optimization	Better ✅	Worse
Generalization	Better ✅	Worse

Momentum 技术

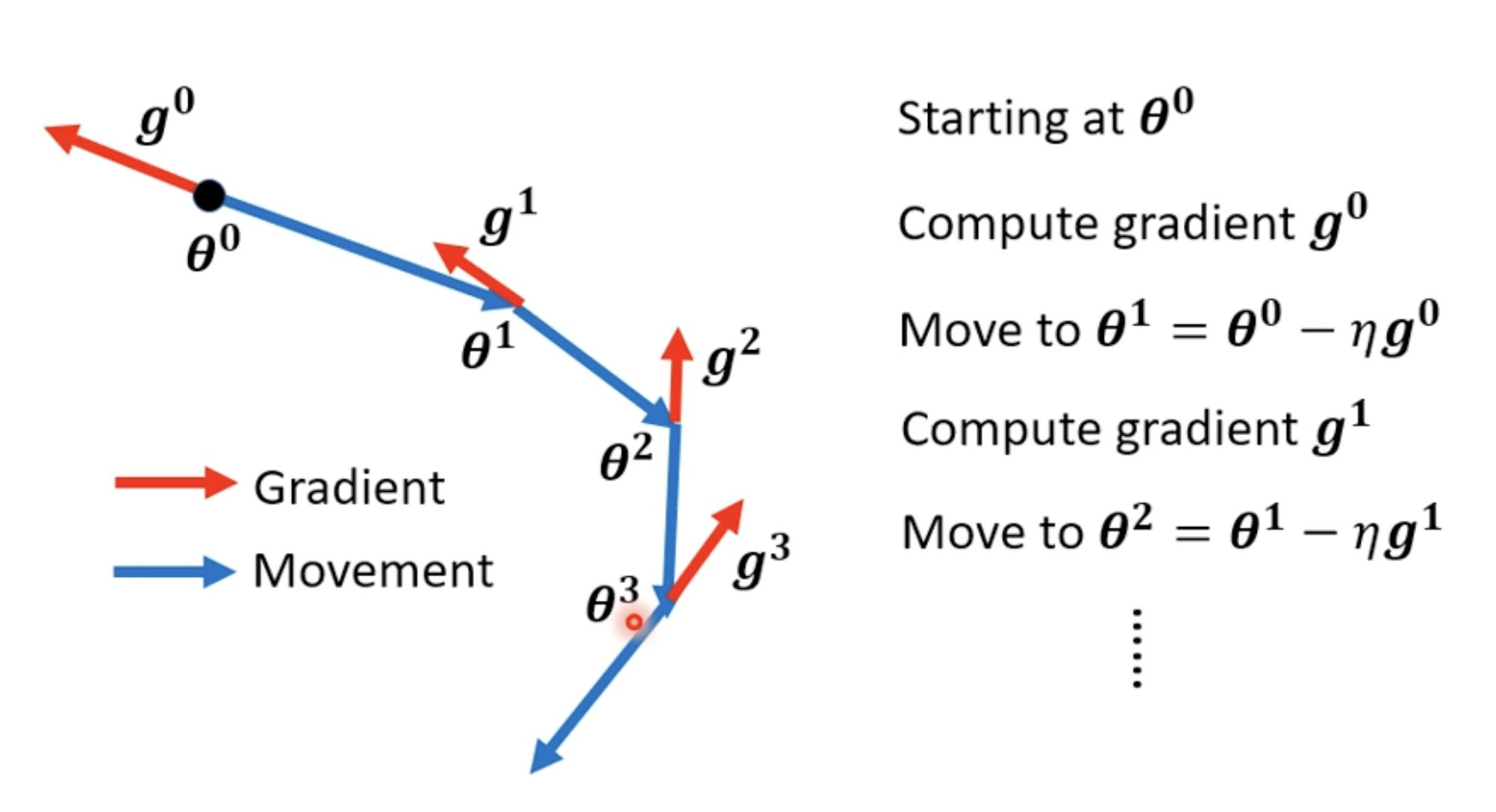
(Vanilla) Gradient Descent

Gradient Descent + Momentum

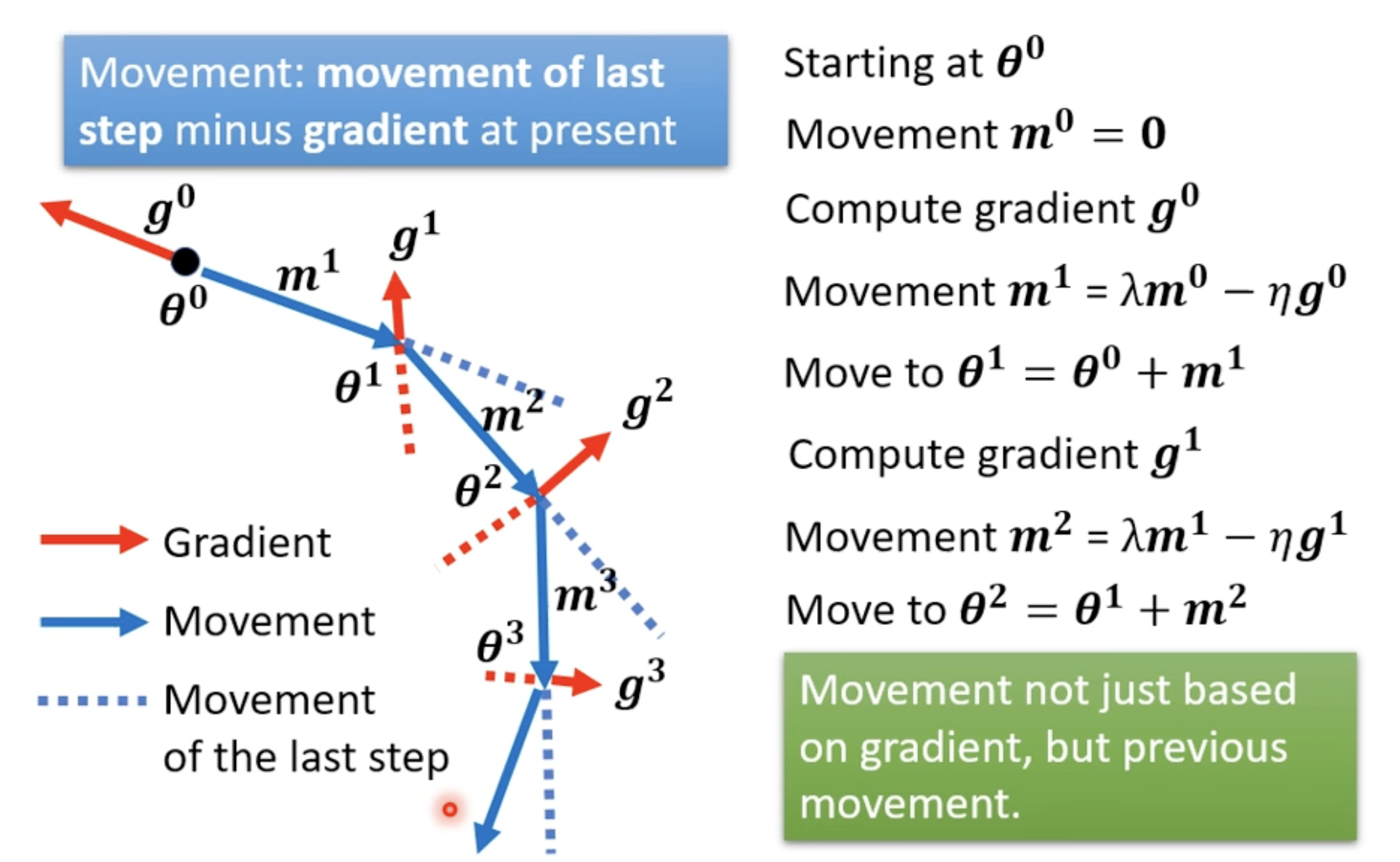
$m^i$ is the weighted sum of all the previous gradient: $g^0, g^1, ..., g^(i-1)$:

$$m^0 = 0$$ $$m^1 = -\eta g^0$$ $$m^2 = -\lambda \eta g^0 - \eta g^1$$ $$...$$

Adaptive Learning Rate 技术

$$[ \theta_i^{t+1} \leftarrow \theta_i^t - \eta g_i^t ]$$ $$[ g_i^t = \left.\frac{\partial L}{\partial \theta_i}\right|_{\theta=\theta^t} ]$$ $$[ \theta_i^{t+1} \leftarrow \theta_i^t - \frac{\eta}{\sigma_i^t} g_i^t ]$$

• $\sigma_i^t$: Parameter dependant

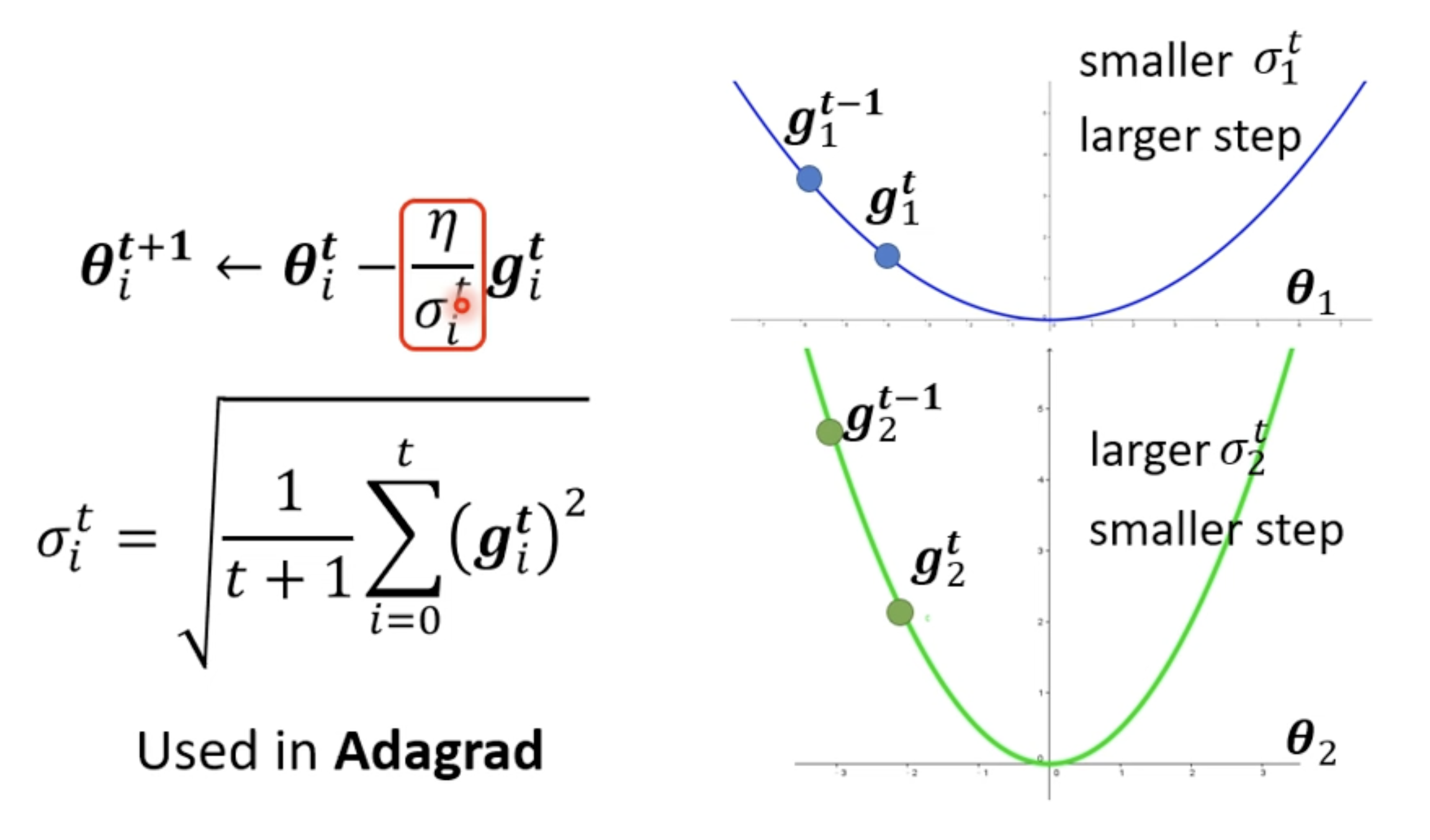
Root Mean Square

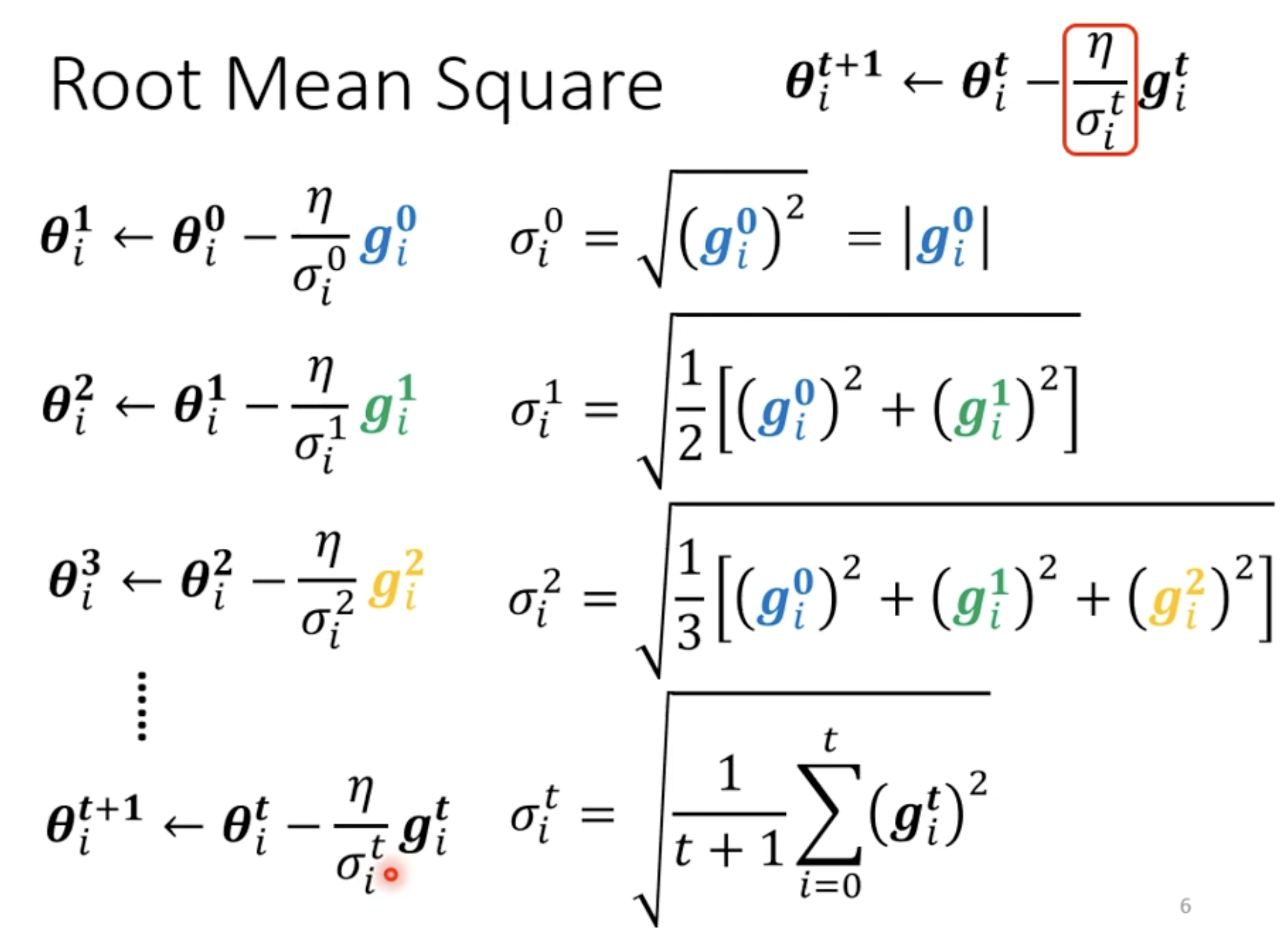
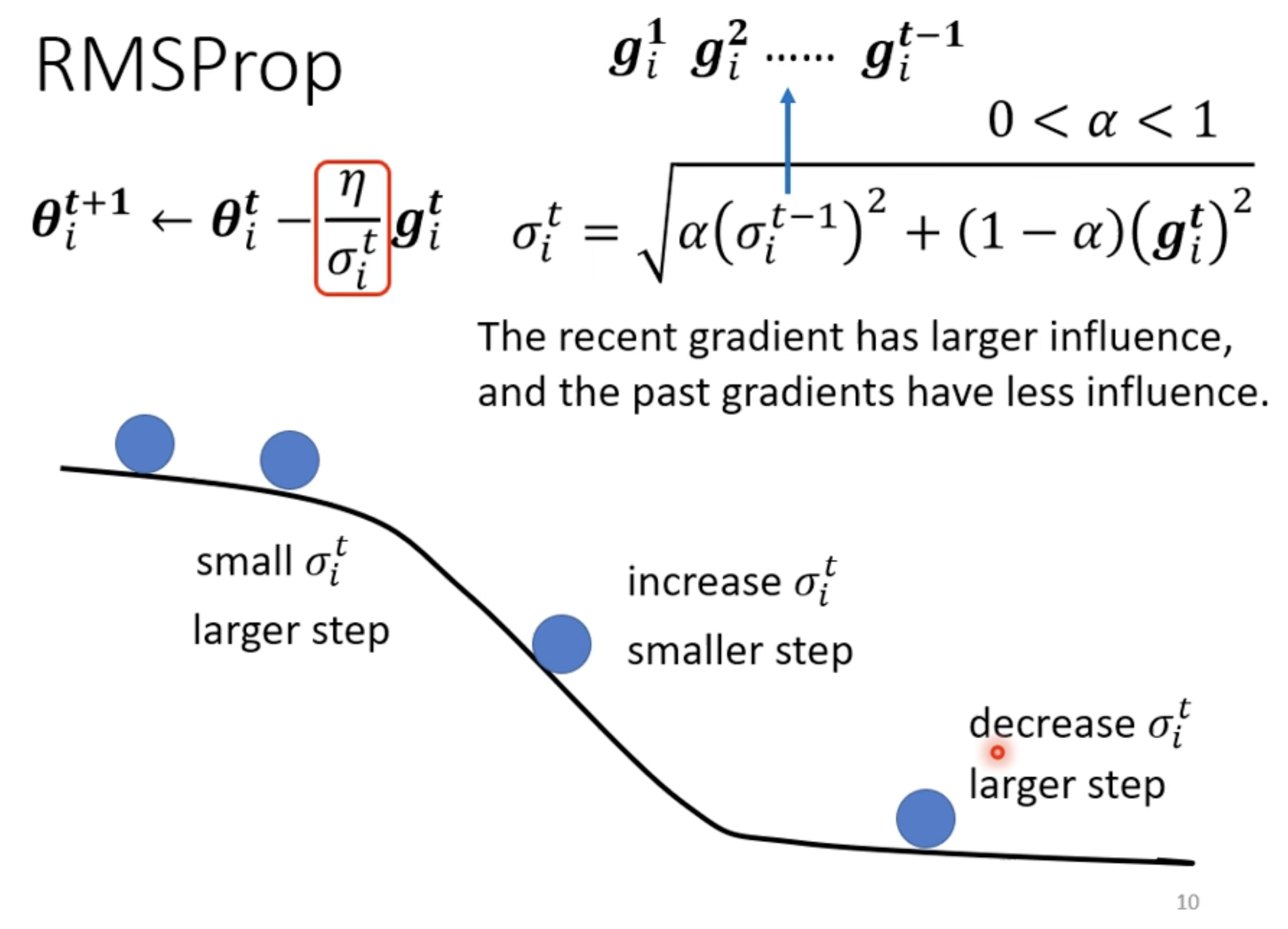
RMSProp

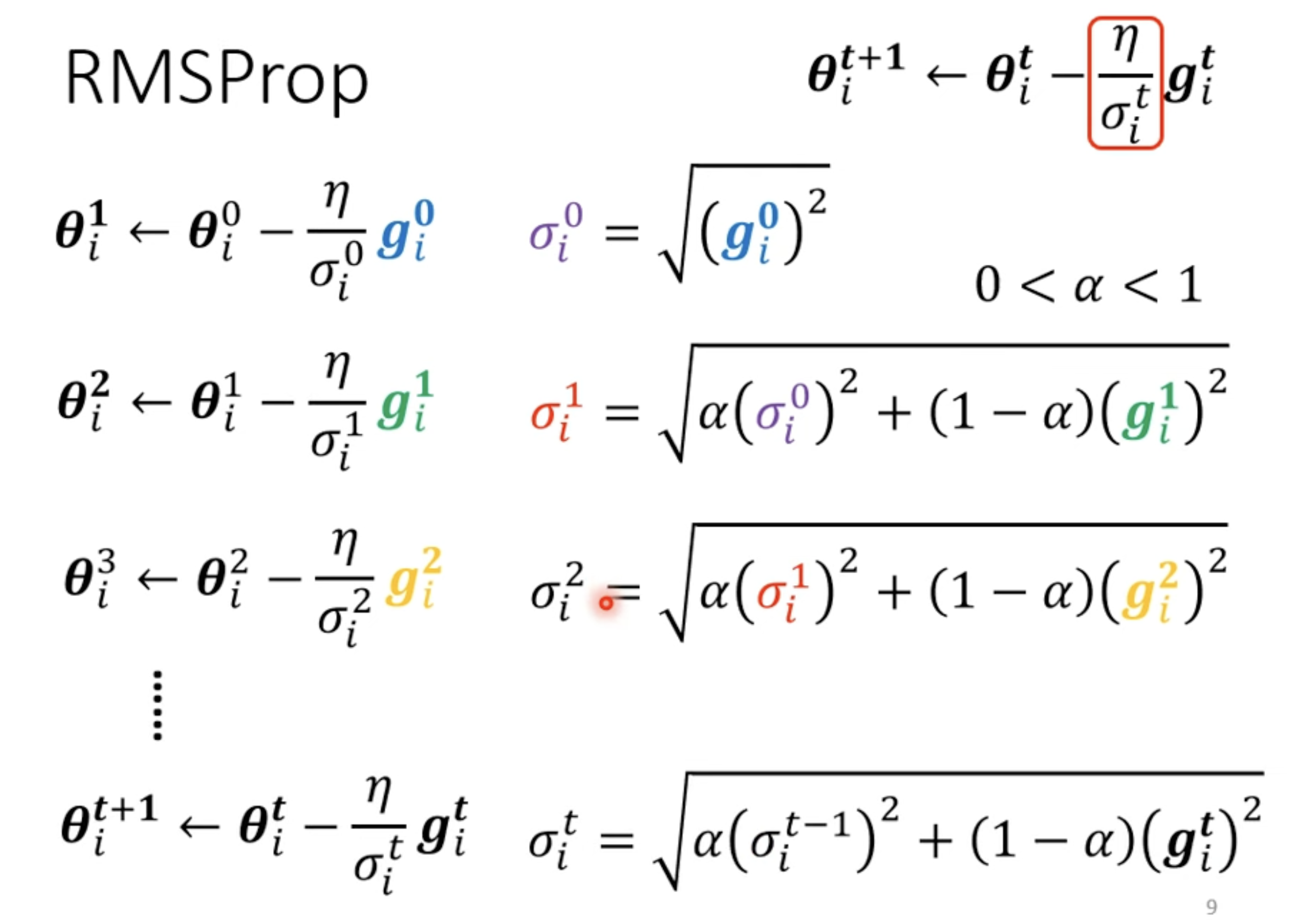
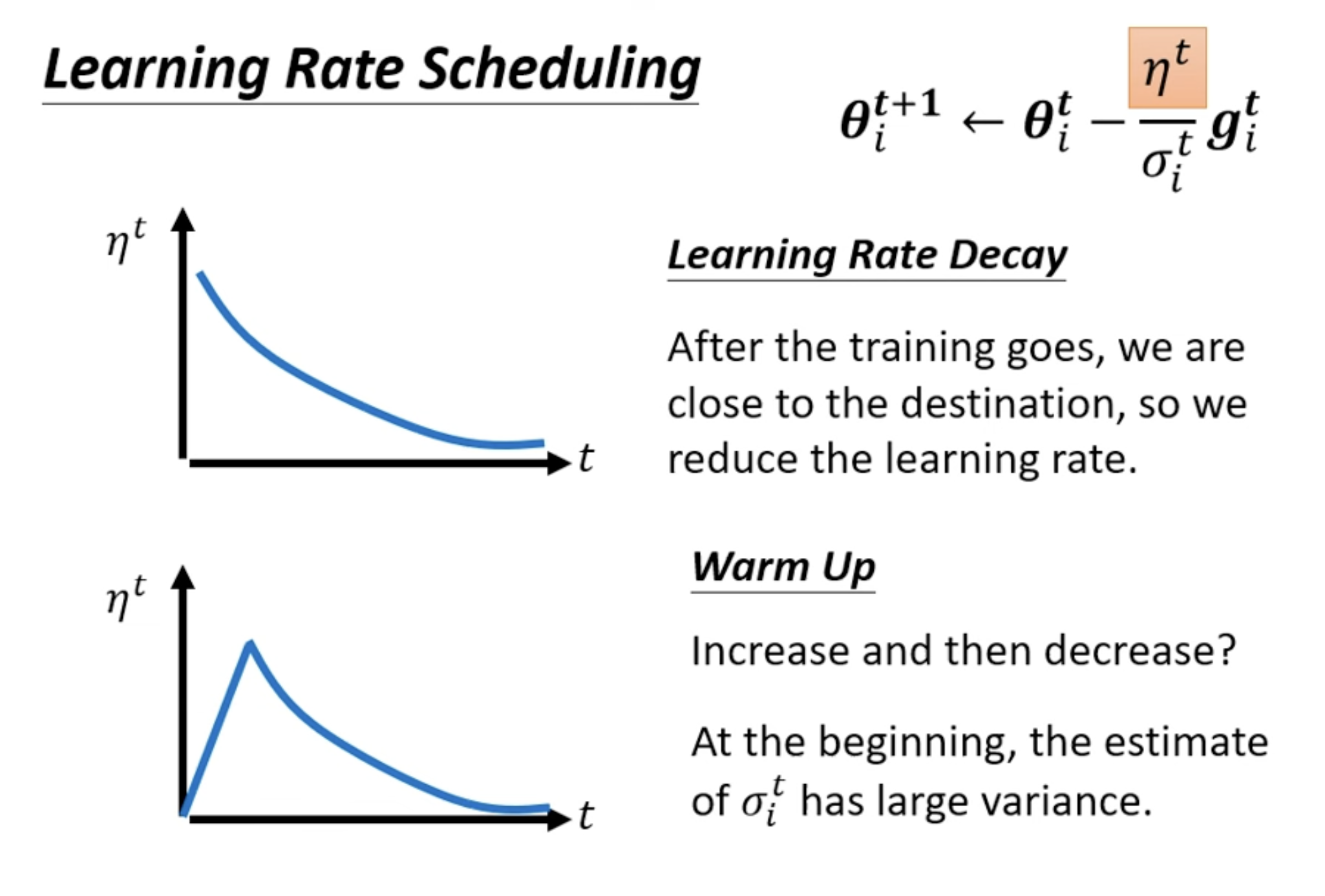
Learning Rate Scheduling

Learning Rate Decay: reduce learning rate by time.