低迭适应 LoRA (zh)
低迭转换 Low-rank transformation
通过将大矩阵分解为两个小矩阵,这两个小矩阵保留有原来大矩阵的所有值,但是值的总数大大少于原矩阵。
-How does LoRA work-step-1-ff2330469f54f085184793412a968e84.png)
训练低迭矩阵
通过训练,我们的低迭矩阵将被更新。
-How does LoRA work-step-2-update new weights-3d427c616a72bb525f44ddb55f4a226e.png)
将两个更新后的低迭矩阵 , 做乘法运算获得与原模型同样大小的权重矩阵。
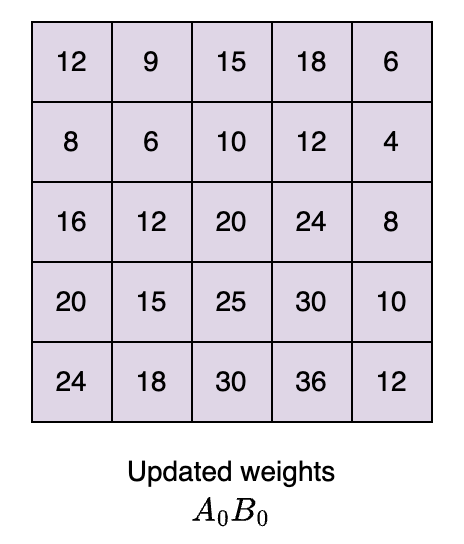
合并原权重矩阵与更新后权重矩阵
公式:
为微调后的模型权重。
-How does LoRA work-step-3-math-function-68166a35d616f2007e09ec457155a751.png)
LoRA 微调参数
Rank
矩阵的迭 rank 定义的是矩阵可以容纳的信息量。它控制权重的精度和可训练参数的数量。选择 rank 的值取决于以下因素:
- 模型大小: 选择矩阵的秩取决于模型的参数数量。如果模型大小很大,则较小的 rank 值也足以捕获信息。但是,如果模型大小较小,则需要高 rank 值来适应模型。
- 任务复杂度:如果任务很简单,那么一个小的 rank 值就足以让模型适应特定的数据,因为它已经拥有很强的一般理解。但是,如果任务很复杂,则需要更高的 rank 值来使模型适应任务复杂性。
- 计算资源:选择矩阵的秩取决于计算资源的可用性。rank 值越高,可训练的参数越多,从而产生更多的训练时间和计算资源。低 rank 值将具有较少的可训练参数。它将减少计算时间和资源。
- 精度级别:在选择等级时,所需的权重精度级别也很重要。与较低的 rank 值相比,较高的 rank 值将具有更精确的权重。
Alpha
对更新后的微调参数进行缩放的参数。
公式:
- 是比例因子。
- r 是矩阵迭 rank。
- > rank:Alpha 的值相对于排名越大,微调权重对模型的影响就越大。当微调数据集与预训练数据不同时,这很有用,我们需要增加微调对模型输出的影响。
- < 等级:Alpha 的值相对于等级越低,微调权重对模型的影响就越小。这将使模型更倾向于预训练的权重。
- = 排名:如果我们的微调数据集很简单,那么理想的情况是保持 等于排名。这通过应用比例因子 来平衡预训练和微调权重对训练模型的影响。
Dropout
Dropout 是一种正则化技术,通过在训练期间关闭模型的某些参数来防止模型过度拟合。它将可训练参数的某些部分随机设置为 0,从而使模型能够在训练数据集上更好地泛化。
- 高 dropout:高 dropout 值(比如 0.1,即 10%)意味着在每批训练期间将丢弃更多低秩矩阵的参数。我们必须小心,因为将 dropout 值设置得太高也会导致欠拟合,即模型没有从训练数据中学到足够的东西。
- 低 dropout:低 dropout 值(例如 0.05,即 0.5%)意味着在每批训练期间将丢弃的低秩矩阵的参数较少。