Graph Algorithms

What is a graph ?

A graph is an abstract notation used to represent the connection between pairs of objects. It can be used to represent networks: systems of roads, airline flights from city to city, how the Internet is connected, or social connectivity on Facebook, Twitter, etc. We use some standard graph algorithms to solve these otherwise difficult problems.

Representing Graphs

Graphs represent pairwise relationships between objects. Graphs are mathematical structures and therefore, can be visualized by using two basic components, nodes and edges.

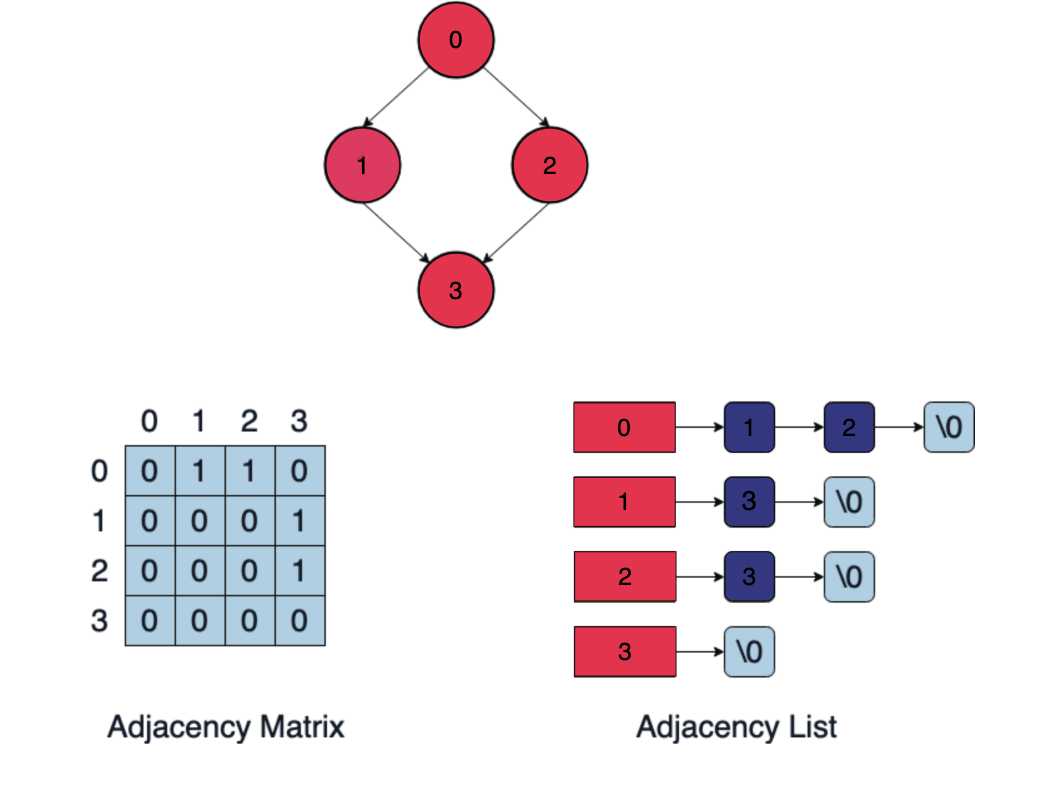
Graphs can be represented as an adjacency matrix or adjacency list.

Adjacency list

An adjacency list is used to represent a finite graph. The adjacency list representation allows you to iterate through the neighbors of a node easily. Each index in the list represents the vertex and each node that is linked with that index represents its neighboring vertices.

Adjacency matrix

An adjacency matrix is a square matrix labeled by graph vertices and is used to represent a finite graph. The entries of the matrix indicate whether the vertex pair is adjacent or not in the graph.

In the adjacency matrix representation, you will need to iterate through all the nodes to identify a node’s neighbors.

Types of graphs

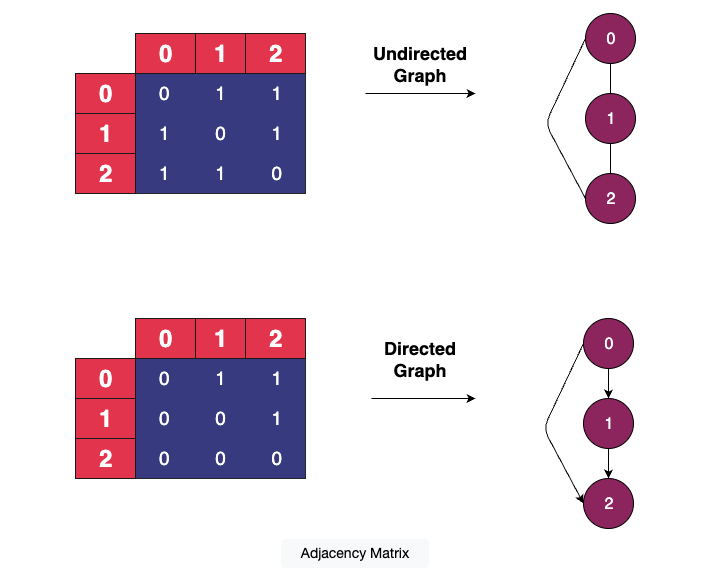
Directed graph

The directed graph is the one in which all edges are directed from one vertex to another.

Undirected graph

The undirected graph is the one in which all edges are not directed from one vertex to another.

Mathematical notation

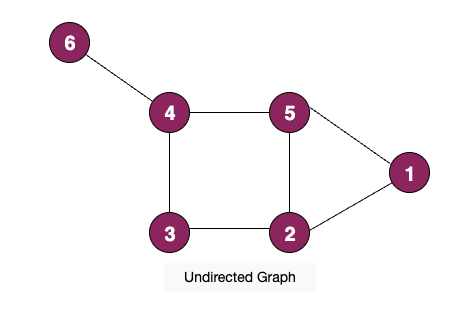
The set of vertices of graph $G$ is denoted by $V(G)$, or just $V$ if there is no ambiguity.

An edge between vertices $u$ and $v$ is written as $u$, $v$. The set of edges of $G$ is denoted $E(G)$, or just $E$ if there is no ambiguity.

The graph in this picture has the vertex set $V = [1, 2, 3, 4, 5, 6]$.

The edge set $E = [[1, 2], [1, 5], [2, 3], [2, 5], [3, 4], [4, 5], [4, 6]]$.

Properties

Path

A path in a graph $G=(V,E)$ is a sequence of vertices $v1,v2,…,vk$, with the property that there are edges between $vi$ and $vi+1$. We say that the path goes from $v1$ to $vk$. The sequence $6,4,5,1,2$ defines a path from node $6$ to node $2$. Similarly, other paths can be created by traversing the edges of the graph. A path is simple, if its vertices are all different.

Cycle

A cycle is a path $v1,v2,…,vk$ for which

1. $k>2$,
2. the first $k−1$ vertices are all different, and
3. $v1=vk$

The sequence $4,5,2,3,4$ is a cycle in the graph above.

Connectedness

A graph is connected, if for every pair of vertices $u$ and $v$, there is a path from $u$ to $v$.

The graph class

The graph class consists of two data members:

1. the total number of vertices in the graph
2. a list to store adjacent vertices

Graph_Class.py

class AdjNode:
    """
    A class to represent the adjacency list of the node
    """

    def __init__(self, data):
        """
        Constructor
        :param data : vertex
        """
        self.vertex = data
        self.next = None

class Graph:
    """
    Graph Class ADT
    """

    def __init__(self, vertices):
        """
        Constructor
        :param vertices : Total vertices in a graph
        """
        self.V = vertices
        self.graph = [None] * self.V

    def add_edge(self, source, destination):
        """
        add edge
        :param source: Source Vertex
        :param destination: Destination Vertex
        """

        # Adding the node to the source node
        node = AdjNode(destination)
        node.next = self.graph[source]
        self.graph[source] = node

        # Adding the source node to the destination if undirected graph

        # Intentionally commented the lines
        #node = AdjNode(source)
        #node.next = self.graph[destination]
        #self.graph[destination] = node

    def print_graph(self):
        """
        A function to print a graph
        """
        for i in range(self.V):
            print("Adjacency list of vertex {}\n head".format(i), end="")
            temp = self.graph[i]
            while temp:
                print(" -> {}".format(temp.vertex), end="")
                temp = temp.next
            print(" \n")

# Main program
if __name__ == "__main__":

    V = 5  # Total vertices
    g = Graph(V)
    g.add_edge(0, 1)
    g.add_edge(0, 4)
    g.add_edge(1, 2)
    g.add_edge(1, 3)
    g.add_edge(1, 4)
    g.add_edge(2, 3)
    g.add_edge(3, 4)

    g.print_graph()

output

Adjacency list of vertex 0
 head -> 4 -> 1

Adjacency list of vertex 1
 head -> 4 -> 3 -> 2

Adjacency list of vertex 2
 head -> 3

Adjacency list of vertex 3
 head -> 4

Adjacency list of vertex 4
 head

We’ve laid down the foundation of our graph class. The variable V contains an integer specifying the total number of vertices.